Solving Equations

ax=b
3x = 0.6 <-- you need to divide both sides by 3
3x/3 = 0.6/3
x=0.2

LS RS check ;
3x=0.6
3(0.2)
0.6

x/a = b <-- you can multiply (a)(b)
x/5 = 0.3
5(x/5) = 5(0.3)
x = 1.5

LS RS check ;
x/5 = 0.3
x = 1.5/0.3

a/x = b
3.3/x = 1.1
x(3/3) = 1.1x
3.3/1.1 = 1.1x/1.1
3=x <--You can do it like this or ...
x=3 <-- this is the more proper way

LS RS ;
3.3/x = 1.1
3.3/3
1.1

2x = 3/4
Divide 2 by itself = 3/4 . 2/1
x = 3/4 x 1/2 . 2/1 x 1/2 makes 0.
3/4 x 1/2 = 3/8

LS RS check ;
2x = 3/4
2/1(3/8) =
6/8
3/4.

another way to the previous question is ...
2x/1 = 3/4
(2x)(4) = 3
8x/8 = 3/8
x = 3/8

-2 1/2x = -3 1/2 <-- make into a proper fraction
-5/2x = -7/2
x = -7/-5

another way of doing it ;
-5/2x = -7/2
-5/2 x -2/5
x = 7/5

and another way ...
-5/2x = -7/2
-5x(2) = 2(-7)
-10x/-10 = -14/-10
x = 14/10 or 7/5

YOUR HOMEWORK:
Read Pages 292-300
Do SYU
Do CYU#3
Practise, APPLY ALL
Extend 3/5
8.1 Homework Book

More Practice on Chapter 7

Today in math class we did different kinds of questions that will be on the test.




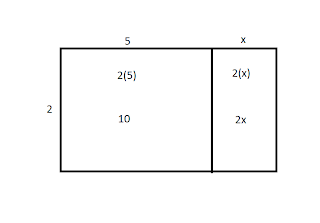
First we were given a question to find the area of rectangle with a missing piece using polynomials.





There are two ways to figuring out the area of this shape. First way is to break up the shape into 3 pieces, and add Areas 1 and 2, and subtract area 3.







The second way is to pretend the missing piece is there (area 1) so it makes a whole rectangle, then subtract area 2 (missing piece) to area 1. I chose to do this method because it seemed like a faster way for me.



Show your work:
l = 8x - 4 + 4x + 9 = 12x +5
w = 6x + 2 + 3x - 5 = 9x - 3

A1 = lw
= (12x + 5)(9x -3)
= (12x)(9x) + (12x)(-3) + (5)(9x) + (5)(-3)
= 108x^ - 36x + 45x - 15

A2 = lw
= (8x - 4)(3x -5)
= (8x)(3x) + (8x)(-5) + (-4)(3x) + (-4)(-5)
= 24x^ - 40x -12x + 20
= 24x^ - 52x + 20

A1 - A2
= 108x^ + 9x -15 - (24x^ - 52x + 20)
= 108x^ +9x - 15 -24x^ +52x - 20
= 84x^ + 61x -35

Therefore, the area of the shape is 84x^ + 61x - 35.


The second question was a triangle. This was much simpler because it didn't contain a missing piece.

A = bh/2
= (8x +4)(5x)/2
= (8x)(5x) + (4)(5x)
= 40x^ + 20x/2
= 40x^/2 + 20x/2
= 20x^ + 10x

The area of the triangle is 20x^ + 10x.

The third question was to find the width of the rectangular prism.

V = lwh
48x³ = (2x)(w)(3x)
48x³ = 6x^
w = 48x³/6x^
w = 8x


The width of the rectangular prism is 8x.




The fourth question is similar to the first one, except with different values. Again, I used the A1-A2 method.





Step 1







Step 2






Step 3






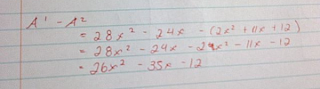
The area of the shape is 26x^ - 35x - 12.


The fifth question is finding the ratio of the rectangle to the circle. This won't be on the test but it's better to know it now for future references.

r = d/2
r = 6x/2
r = 3x

rectangle / circle
= lw / pi r^
= 6x(12x) / pi(3x)^
= 72x^/pi 9x^
= 8 / pi



The last question was to find the ratio of the small circle to the large circle.

So/Lo = pi r^/pi r^
= pi(2x)^/pi(4x)^
= 4x^/16x^
= 4/16
= 1/4






Solve:
1. 3(5x + 3) - (10x - 6)
= 15x +9 - 10x + 6
= 5x + 15

2. (1/2t)^ 3t
= (1/2t)(1/2t)(3t)
= 1/4t^(3t)
= 3/4t³


Remember:
Always use the FOIL(First, Outside, Inside, Last) method when multiplying
Only add/subtract like terms
When subtracting polynomials, (-) before the 2nd polynomial means to multiply (-1) to each term. (Change each sign to its opposite)
Study, go on Mangahigh, and practice!

The next person to do the scribe will be Jocelle Garcia!

Diorella's Blog Post

Sorry about my blog being all pictures.

HOMEWORK:

Green sheet 7.6 & 7.11

MANGA HIGH

The next person to do the blog will be.. Marie Domingo.

Mark C's Multiplying Binomials & Dividing Post

Click here for a website that teaches and reviews more things about the FOIL method

DIVISION

HOMEWORK:

Read pp. 272-274

CYU #1 & 2

Practice: Odd/Even

Apply: All

Extend: 2 of 3

Homework Book: 7.3

Green Sheets: 7-10 #1-7

Ryan's math blog post

Today we learned about triangles.

Scalene: all sides, all angles are different

Isosceles: 2 sides, 2 angles the same

Equilateral: all sides, all angles the same

An example of finding the area of a triangle:

We also learned more about solving algebraic expressions.

For example: 2(5+x)= 2(5) + 2(x)

= 10 + 2x

A common mistake is adding or subtracting 10 by 2x because they are unlike terms.

A new diagram for finding the answer of 2(5+x) is:

Inside the box, the top part is the expression and the bottom part is the answer.

Another example is: 2x(3x^2 + 4x -y)

=6x^3 + 8x^2 - 2xy

HOMEWORK

- read page 264-268

-CYU: #2, 3

-Practise: odd/even

-Apply: all

-2 of 3 extend

-7.2 homework book

-Green sheet:7-4

The next person doing the blog is Brandon Arano.

Multiplying and Dividing Monomials.

In class we learned how to multiply and divide monomials. We started off by doing some easy integer questions.

Multiplying monomials:

To start off we did a four questions they were:

(3)(2)= 6

(-4)(4)= -16

(-7)(-3)=21

(5)(-6)= -30

then we got to harder questions

3(2x)= 6x "this means 3 groups of 2x"

we had to model it after wards

-4(3x)=-12x

(-3y)(-2x)= 6xy

"I think that the answer turned out to be xy because if you multiply two numbers with different variables you're answer has to have a degree of two."

(3x)(-3x) = -9x^2 (squared)

"This is one became squared because if you multiply two variables and they are both the same you get 2nd degree or squared"

Dividing Monomials:

Similar to Multiplication we had to do some questions.

6/3= 3

-8/4=(-2)

16/-8= -2

-15/-3= 5.

6x/3= 2x

How to model division monomials.

very similar to the multiplication model.

-4xy/-2x= 2y

"how?''

'' since there are two x's both of them get canceled out, leaving you with just the variable y''

-6y^2/2y= -3y

"since there were two y's on the first one, one gets canceled out and only one is left"

Not everything can get modeled for example:

-6^3/ -2x= 3x^2

"The reason for that is because we don't have anything to represent a cube."

HOMEWORK!!!

7.1 read pp 254-259

CYU#2

Practise : odd/even

Apply: all

Extend : 24,26,27

Homework book :7.1

" The next scribbler is Ryan Bautista"

Rise and Run

January 27, 2012's class

Chapter 6

In class we learned more about finding the equation of a graph using rise and run. We had many examples.

Now we know what m is, we can put that in our equation to find y.

y=mx+b

Remember the m is the slope or gradient and the b is the y intercept.

The m will be 4/7 and the b will be 1.

y=4/7x+1

We put the results in a table:

Here's how we got the y using the equation:

y=mx+b

=4/7x+1

= 4/7(1)+1 (you multiply 4/7 by 1)

=4/7+1 (you add 1 to 4/7)

=1 4/7

y=mx+b

=4/7x+1

=4/7(2)+1

=8/7=1 (simplify 8/7 to 1 1/7)

=1 1/7+1

=2 1/7

We also did a problem where b=0.

Since b=0, then in the equation there doesn't need to be +b. We used 1 and 14 for x.

y=mx

=2/3x

=2/3(1)

=2/3

y=mx

=2/3x

=2/3(14)

=28/3 (simplify 28/3 to 9 1/3)

=9 1/3

You call them by where they go through the line

Homework

Chapter 6.3

-all practice

-all apply

-try any 2 of extend

-Homework Book

-Save your Dumb Planet

-CYU question1 due monday

-MANGAHIGH!!

                     

  HOMEWORK:
READ PAGE 220-225
CYU 1 hand in for marks 
PRACTICE ADD OR EVEN
EXTEND ONE OF E`M
6.2 HANDBOOK
MANGAHIGH !!!
DERECK WILL BE DOING THE NEXT BLOG ..

Chapter 6 Linear Equations

Linear Relation y=m x+b

Linear Equation y=m x-b

Ordered Pairs

Ordered Pairs have order that is (xy)

Cartesian Plane

Coordinate Grid

Dependent

Independent

Tables

Choice

y=m x+ 6

6=2 2t+2

Chairs for 15th table?

6=2t+2

c=2t+2

=2(15)+2

=30t+2

=32

32 chair for the 15th table.

6=2t+26=2t+2

c=2t+2c=2t+2

Leg=5

Perimeter

Perimeter of the 17th triangle

A Perimeter

P=5t+15

=5(17)+15

=85+10

=95

The 25th set has how many marbles?

M=2s+3

=2(8)+3

=2(8)+3

=59

HOMEWORK

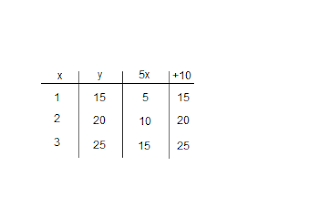
• 6.1 Read pp. 2-16
• Key Ideas
• CYU #2,3
• Practice Odd or Even
• Apply All
• Extend #17 and 15 or 16
• Homework Book Get Ready

The next person who will do the blog is

Rowell Cabate
Mangahigh

Brandon's Blog Post

Adding Integers:

Positive added to positive is always positive, adding negative to negative is negative also. Adding to positive, keep sign of integer with greatest absolute value. positive added to negative do as negative added to positive.

Here are some examples:

1) 1+1 = 2

2) -2+-2 = -4

3) -3+2 = -1

4) 5+-2 = 3

Multiplying Integers:

Positive multiplied with positive is positive, however negative multiplied by negative is positive, negative multiplied with positive is negative, and positive multiplied by negative is always negative.

Here are some examples:

1) (2)(2) = 4

2) (-6)(-2)= 12

3)(-3)(3)= -9

4) (3)(-3)= -9

Adding and subtracting like terms:

6x²+3x-4y+5+5y+6x-7x²-7 (Remember that colours represent like terms)

Step 1 ) Collect like terms in order of degree and alphabet.

6x²-7+3x+6x-4y+5y+5-7

Step 2) Simplify

-x²+ax+y-2.

Removing brackets when combining like terms:

(4x+3) + (-6x-3)

Step 1) Look at the sign (+,-) in front of each bracket, if it is a (+) leave the signs in the bracket the same, remove the (+) and rewrite the question.

Example:

4x+3-6x-3

Step 2) Combine like terms

4x-6x+3-3

Step 3) Simplify

-2x

Here's another one:

(-3x+4) + (+5x-7) = -3x+4+5x-7

= -3x+5x+4-7

= 2x-3

(Remember to always write your work on the right!)

Combining like terms with negative brackets:

(-6x+7) - (-4x+2)

Step 1) Look at the sign (+,-) in front of each bracket, if it is a (-), multiply each term by negative one

-6x+4x4+7-2

Step 2) Combine like terms

-6x+4x+7-2

Step 3) Simplify

-2x+5

HOMEWORK !

Manga high

read pages 183-186

CYU #2, #4

Practice odd or even

apply # 13-22

Extend # 23-25

Page 2 Interaction sheet

Why did the donkey get a passport?

Why is it good to play cards in a graveyard?

The next person that will be doing the blog is

BJ Alcantara

p.s the colours and sizes won't work on my post.

Degrees and Terms

Degree of a term: Is the sum of it's exponents.

Examples:

1. 
2. 
3. 
4. 

Degree of a polynomial: Is the greatest degree of any of the terms in a polynomial

Examples:

1. 
2. 

Like terms will have the same variables and the same degree of variable or be constant

Example: 6x^2 - 3x^2y

Unlike terms do not share a common variable or degree of variable

Example: 6xy^2 - 3x^2y

Textbook work:

• CYU #1, 3, and 4
• Prac: # 5-12
• Apply #15, 17 and 19
• Extend #28, 29 and 31
• 5.1 EXTRA PRACTICE
• AND MANGA HIGH!!