Julibella's Blog Post

Review:
How do we prove the triangles are the same?


-if the angles are the same
AAA (angle angle angle law)

-if the sizes are the same
ASA (angle side angle law)

-if the sides and angles are the same.
SAS (side angle side law)

-if the side and side and side equal
SSS (side side side law)

2/4 = 1/2 = 3/6 = 0.5 or 1/2
or you could write it the opposite way:
6/3 = 2/1 = 4/2
It will still equal the same thing:
0.5 or 1/2

*As long as you are comparing "this" to "that".

Is this triangle the same as well?

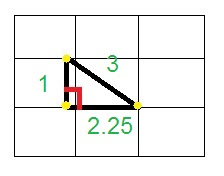
No, because not all the angles are the same. The sides are not equivalent to the original shape.



Next Unit: Polygons

Definition of a polygon: 2D shape that is a closed figure made of 3 or more line segments.

This unit will be focusing on identify similar polygons and explain why they are similar. Drawing similar polygons. Solving problems using the properties of similar polygons.



Don't forget to check out COOL MATH SITES on the blog.
Also remember to revisit Similarity and Proportions

Homework:
-Go to Mr. Backé 's site <!--> Normal 0 false false false EN-US X-NONE X-NONE

-Textbook: Chapter 4.4
Practice #3, 5, 6
All Apply
Extend any 3 #13-17
Homework Book Chapter 4.4
Extra Practice 4.4

-Mangahigh

SCALE

Ø is a comparison of two objects; the actual size and its diagram

Ø Scale can be expressed as a ratio (most common), as a fraction, as a percent, in words or as a diagram.

A scale of 1:50 means that 1 unit on the diagram is equal to 50 units of the actual object.

SCALE DIAGRAM

Ø Is similar or the actual or object. It maintain proportion, the diagram may be longer or smaller than the actual object.

There are two ways to find a missing length of proportion:

Example One: Use scale to determine the Actual Length of an Object.

For a scale of 1:14 and a diagram measuring 5.5cm set the proportion.

       SCALE

Ø is a comparison of two objects; the actual size and its diagram

Ø Scale can be expressed as a ratio (most common), as a fraction, as a percent, in words or as a diagram.

A scale of 1:50 means that 1 unit on the diagram is equal to 50 units of the actual object.

SCALE DIAGRAM

Ø Is similar or the actual or object. It maintain proportion, the diagram may be longer or smaller than the actual object.

There are two ways to find a missing length of proportion:

Example One: Use scale to determine the Actual Length of an Object.

For a scale of 1:14 and a diagram measuring 5.5cm set the proportion.

                  x= 5.5(14)

                   x=77cm

Because it is easy to find the relationship of 1 to 5.5 it easy to find x, simply multiply 14 by 5.5 to find x=77cm- So the actual object is 77cm.           x= 5.5(14)

                   x=77cm

Because it is easy to find the relationship of 1 to 5.5 it easy to find x, simply multiply 14 by 5.5 to find x=77cm- So the actual object is 77cm.

Example Two: Use Measurement to find Scale

An object measures has an actual measurement of 120 km. What is the scale?

      Set up a proportion: 1 km= 100000cm

 

So the scale is 1:2400000cm or 1:24km


HOMEWORK: ALL OF THE WORKSHEET & TEXTBOOK 
                        WORKBOOK 
                        MANGAHIGH CHALLENGE 

An enlargement is to make bigger. In mathematics we would need to multiply by a factor greater than one.

Example:
6 x 1.2
3 x 2
4 x 4

A reduction is to make smaller. In mathematics we would need to multiply by a factor less than one but greater than zero.

Example:
6 x 0.9
5 x 0.4
7 x 0.8


Scale factor- The constant factor by which all dimension of object are to be enlarged or reduced in a scale drawing.






If a rectangle that is (3x5) is to be enlarge by a scale factor of 1.3, What are it's new dimension?


3.9 x 6.5

3 x 1.3= 3.9
5 x 1.3= 6.5

If the same rectangle (3x5) is to be reduce by a scale factor of 0.6, What are the new dimension? 1.8 x 3

3 x 0.6= 1.8
5x 0.6= 3


To make an enlargement or reduction it must be proportional. That is, it must maintain it's original shape, but not it's size.





Enlargements and reductions can also be made using diffirent sized graph paper. Artist often use this method when drawing large murals from a small original.

Mark's "Using Exponents to Find Area" Post

They all use exponents to find the Surface Area.

Use Reciprocals to answer questions like this.

HOMEWORK:

2.4 Show You Know

Check Your Understanding - 1, 2

Practice Odd or Even - Apply All

Extend #13

Homework Book

Extra Practice

Manga High Challenges

BJ will be doing the next blog.